Two-dimensional meshless solution of the non-linear convection diffusion reaction equation by the Local Hermitian Interpolation method
Main Article Content
Keywords
Radial Basis Functions, Meshless methods, Symmetric method, Newton Raphson, Homotopy Analysis Method.
Abstract
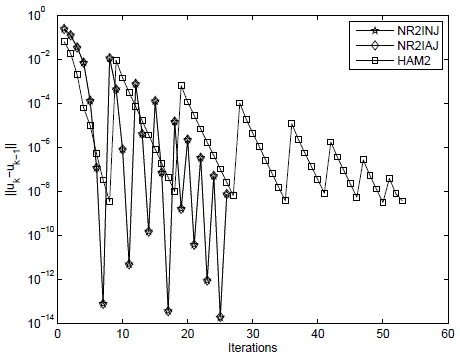
A meshless numerical scheme is developed for solving a generic version of the non-linear convection-diffusion-reaction equation in two-dimensional domains. The Local Hermitian Interpolation (LHI) method is employed for the spatial discretization and several strategies are implemented for the solution of the resulting non-linear equation system, among them the Picard iteration, the Newton Raphson method and a truncated version of the Homotopy Analysis Method (HAM). The LHI method is a local collocation strategy in which Radial Basis Functions (RBFs) are employed to build the interpolation function. Unlike the original Kansa’s Method, the LHI is applied locally and the boundary and governing equation differential operators are used to obtain the interpolation function, giving a symmetric and non-singular collocation matrix. Analytical and Numerical Jacobian matrices are tested for the Newton-Raphson method and the derivatives of the governing equation with respect to the homotopy parameter are obtained analytically. The numerical scheme is verified by comparing the obtained results to the one-dimensional Burgers’ and two-dimensional Richards’ analytical solutions. The same results are obtained for all the non-linear solvers tested, but better convergence rates are attained with the Newton Raphson method in a double iteration scheme.
MSC: 65H20, 65N35
Downloads
References
[2] E. J. Kansa, “Multiquadrics -a scattered data approximation scheme with applications to computational fluid dynamics-II solution to parabolic, hyperbolic and elliptic partial differential equations,” Comput. Math. Appl., vol. 19, no. 8-9, pp. 127–145, 1990. 23
[3] F. E. Fasshauer, “Solving partial differential equations by collocation with radial basis functions,” Surf. Fit. Multires. Methods, pp. 131–138, 1997. 23, 24, 29
[4] B. Jumarhon, S. Amini, and K. Chen, “The Hermite collocation method using radial basis functions,” Eng. Anal. Boundary Elem., vol. 24, no. 7-8, pp. 607–611, 2000. 23, 31
[5] H. Power and V. Barraco, “A comparison analysis between unsymmetric and symmetric radial basis function collocation methods for the numerical solution of partial differential equations,” Comput. Math. Appl., vol. 43, no. 3-5, pp. 551–583, 2002. 23, 31
[6] A. LaRocca, A. Hernandez, and H. Power, “Radial basis functions Hermite collocation approach for the solution of time dependent convenction-diffusion problems,” Eng. Anal. Boundary Elem., vol. 29, no. 4, pp. 359–370, 2005. 24, 30
[7] P. P. Chinchapatnam, K. Djidjeli, and P. B. Nair, “Unsymmetric and symmetric meshless schemes for the unsteady convection?diffusion equation,” Comput. Meth. Appl. Mech. Eng., vol. 195, no. 19–22, pp. 2432–2453, 2006. 24
[8] W. R. Madych and S. A. Nelson, “Multivariate Interpolation and Conditionally Positive Definite Functions,” Math. Comput., vol. 54, no. 1, pp. 211–230, 1990. 24
[9] M. Zerroukat, H. Power, and C. S. Chen, “A numerical method for heat transfer problems using collocation and radial basis functions,” Int. J. Numer. Methods Eng., vol. 42, no. 7, pp. 1263–1278, 1998. 24
[10] J. Li, A. H. D. Cheng, and C. S. Chen, “A comparison of efficiency and error convergence of multiquadric collocation method and finite element method,” Eng. Anal. Boundary Elem., vol. 27, no. 3, pp. 251–257, 2003. 24
[11] A. H.-D. Cheng and J. J. S. P. Cabral, “Direct solution of ill-posed boundary value problems by radial basis function collocation method,” Int. J. Numer. Methods Eng., vol. 64, no. 1, pp. 45–64, 2005. 24
[12] S. Chantasiriwan, “Cartesian grid methods using radial basis functions for solving Poisson, Helmholtz, and diffusion?convection equations,” Eng. Anal. Boundary Elem., vol. 28, no. 12, pp. 1417–1425, 2004. 24
[13] R. Schaback, “Multivariate interpolation and approximation by translates of basis functions,” Approx. Theory, vol. 8, pp. 1–8, 1995. 24
[14] D. Brown, “On approximate cardinal preconditioning methods for solving PDEs with radial basis functions,” Eng. Anal. Boundary Elem., vol. 29, pp. 343–353, 2005. 24
[15] L. Ling and R. Schaback, “On adaptive unsymmetric meshless collocation,” Proceedings of the 2004 international conference on computational and experimental engineering and sciences, 2004. 24
[16] C. Lee, X. Liu, and S. Fan, “Local Multicuadric approximation for solving boundary value problems,” Comput. Mech., vol. 30, pp. 396–409, 2003. 24
[17] B. Sarler and R. Vertnik, “Meshless explicit local radial basis function collocation methods for diffusion problems,” Comput. Math. Appl., vol. 51, pp. 1269–1282, 2006. 24, 25
[18] E. Divo and K. Kassab, “An efficient localised radial basis function collocation method for fluid flow and conjugate heat transfer,” J. Heat Transfer, vol. 212, pp. 99–123, 2006. 24, 25
[19] G. Wright and B. Fornberg, “Scattered node compact finite difference-type formulas generated from radial basis functions,” J. Comput. Phys., vol. 212, no. 1, pp. 99–123, 2006. 24
[20] C. K. Lee, X. Liu, and S. C. Fan, “Local multiquadric approximation for solving boundary value problems,” Comput. Mech., vol. 30, no. 5-6, pp. 396–409, 2003. 24
[21] T. J. Moroney and I. W. Turner, “A finite volume method based on radial basis functions for two-dimensional nonlinear diffusion equations,” Appl. Math. Modell., vol. 30, no. 10, pp. 1118–1133, 2006. 25
[22] ——, “A three dimensional finite volume method based on radial basis functions for the accurate computacional modelling of nonlinear diffusion equations,” J. Comput. Phys., vol. 225, no. 2, pp. 1409–1426, 2007. 25
[23] P. Orsini, H. Power, and H. Morovan, “Improving Volume Element Methods by Meshless Radial Basis Function Techniques,” Comput. model. Eng. Scien., vol. 769, no. 1, pp. 1–21, 2008. 25
[24] D. Stevens, H. Power, and H. Morvan, “An order-N complexity meshless algorithm for transport-type PDEs,based on local Hermitian interpolation,” Eng. Anal. Boundary Elem., vol. 33, no. 4, pp. 425–441, 2009. 25, 28, 31, 32
[25] D. Stevens, H. Power, M. Lees, and H. Morvan, “The use of PDE centres in the local RBF Hermitian method for 3D convective-diffusion problems,” J. Comput. Phys., vol. 228, no. 12, pp. 4606–4624, 2009. 25, 28, 29, 30, 31
[26] B.-C. Shin, M. T. Darvishi, and C.-H. Kim, “A Comparison of the Newton-Krylov method with high order Newton-like methods to solve nonlinear
systems,” Appl. Math. Comput., vol. 217, no. 7, pp. 3190–3198, 2010. 25, 32, 43
[27] Y. I. Kim and Y. H. Geum, “A cubic-order variant of Newton’s method for finding multiple roots of nonlinear equations,” Comput. Math. Appl., vol. 62, pp. 1634–1640, 2011. 25
[28] X. Cui and J.-Y. Yue, “A nonlinear iteration method for solving a twodimensional nonlinear coupled system of parabolic and hyperbolic equations,” J. Comput. Appl. Math., vol. 234, no. 2, pp. 343–364, 2010. 25
[29] P. S. Mohan, P. B. Nair, and A. J. Keane, “Inexact Picard iterative scheme for steady-state nonlinear diffusion in random heterogeneous media,” Phys. Rev. E, vol. 79, no. 4, pp. 1–9, 2009. 25
[30] D. Stevens, H. Power, M. Lees, and H. Morvan, “A Meshless Solution Technique for the Solution of 3D Unsaturated Zone Problems, Based on Local Hermitian Interpolation with Radial Basis Functions,” Transp. Porous Media, vol. 79, no. 2, pp. 149–169, 2009. 25
[31] S. J. Liao, “On the general boundary element method,” Eng. Anal. Boundary Elem., vol. 21, no. 1, pp. 39–51, 1998. 26
[32] ——, “Boundary element method for general nonlinear differential operators,” Eng. Anal. Boundary Elem., vol. 20, no. 2, pp. 91–99, 1997. 26, 35
[33] ——, “A direct boundary element approach for unsteady non-linear heat transfer problems,” Eng. Anal. Boundary Elem., vol. 26, pp. 55–59, 2002. 26, 36
[34] Z. Lin and S. Liao, “The scaled boundary FEM for nonlinear problems,” Commun. Nonlinear Sci. Numer. Simul., vol. 16, no. 1, pp. 63–75, 2011. 26
[35] S. S. Motsa, P. Sibanda, and S. Shateyi, “A new spectral-homotopy analysis method for solving a nonlinear second order BVP,” Commun. Nonlinear Sci. Numer. Simul., vol. 15, no. 9, pp. 2293–2302, 2010. 26
[36] H. Zhu, H. Shu, and M. Ding, “Numerical solutions of partial differential equations by discrete homotopy analysis method,” Appl. Math. Comput., vol. 216, no. 12, pp. 3592–3615, 2010. 26
[37] M. Noskov and M. D. Smooke, “An implicit compact scheme solver with application to chemically reacting flows,” J. Comput. Phys., vol. 203, pp. 700–730, 2005. 38
[38] F. T. Tracy, “Clean two- and three-dimensional analytical solutions of Richards’ equation for testing numerical solvers,” Water Resour. Res., vol. 42, no. 8, pp. 1–11, 2006. 43