Modeling the Availability of a Repairable Series Structure with two Units
Main Article Content
Keywords
Work-mission-availability, semi-Markov model, Markov processes, integral equations system, repairable components
Abstract
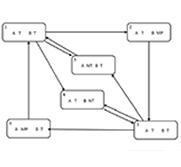
When there is a structure with two serial components where each one owns a life time that is distributed exponentially and both of the components are repairable, it is established a renovation process, in which both components need to be working in order for the operation of the structure. It is observed that the renovation process evidences a semimarkovian behavior and it is shown that through this one, its availability function is one of the inquiries of a system of integral equations that is solved by a numerical method designed for that purpose. The novelty in this article is that it is considered a process whose state space includes repair time, which is useful in engineering applications.
Downloads
References
[1] H. Guo, H. Lia, and W. Zhao, “A new stochastic model for systems under general repairs,” IEEE Transactions on Reliability, vol. 56, no. 01, pp.40–49, 2007. https://doi.org/10.1109/TR.2006.890895
[2] H. Yi and L. Cui, “A study on repairable series systems with markov repairable units,” Springer Series in Reliability Engineering, pp. 121–157, Jan. 2018. https://doi.org/10.1007/978-3-319-63423-4_7
[3] F. Kayedpour, M. Amiri, M. Rafizadeh, and A. S. Nia, “Multiobjective redundancy allocation problem for a system with repairable components considering instantaneous availability and strategy selection,” Reliability Engineering & System Safety, vol. 160, pp. 11–20, Apr. 2017. https://doi.org/10.1016/j.ress.2016.10.009
[4] R. Melo, C. Lara, and F. Jacobo, “Estimación de la confiabilidad disponibilidad-mantenibilidad mediante una simulación tipo monte carlo de un sistema de compresión de gas amargo durante la etapa de
ingeniería,” Tecnología Ciencia, vol. 2, no. 24, pp. 93–104, 2009. https://www.redalyc.org/articulo.oa?id=48213841002
[5] M. N. Alvarez, “Estudio de la fiabilidad de los sistemas reparables y desarrollo de un procedimiento de análisis multivariante,” Ph.D. dissertation, Escuela Técnica Superior de ingenieros Industriales, 2017.
[6] M. Abouei Ardakan, Z. Mirzaei, A. Zeinal Hamadani, and E. A. Elsayed, “Reliability optimization by considering time-dependent reliability for components,” Quality and Reliability Engineering International, vol. 33, no. 8, pp. 1641–1654, 2017. https://doi.org/10.1002/qre.2132
[7] E. López, “Estudio de la fiabilidad de sistemas con reparaciones pospuestas,” Ph.D. dissertation, Universidad de Extremadura, 2004.
[8] A. Csenki, “Joint availability of systems modelled by finite semi-markov processes,” Appl. Stochastic Models & Dam Analysis, vol. 10, pp. 279–293, 1994. https://doi.org/10.1002/asm.3150100406
[9] A. Csenki, “Mission availability for repairable semi-markov systems: analytical results and computational implementation,” Statistics, vol. 26, pp. 75–87, 1995. https://doi.org/10.1080/02331889508802468
[10] A. Csenki, “Transient analysis of interval availability for repairable systems modelled by finite semi-markov processes,” IMA J. Math. Appl. in Business and Industry, vol. 6, pp. 267–281, 1995. https://doi.org/10.1093/imaman/6.3.267
[11] L. Donatiello and B. R. Lyer, “Closed-form solution for system availability distribution,” IEEE Trans. Reliab, vol. 36, pp. 45–47, 1987. https://doi.org/10.1109/TR.1987.5222291
[12] G. Rubino and B. Sericola, “Interval availability analysis using operational periods,” Performance Evaluation, vol. 14, pp. 257–272, 1992. https://doi.org/10.1016/0166-5316(92)90008-5
[13] S. Alaswad and Y. Xiang, “A review on condition-based maintenance optimization models for stochastically deteriorating system,” Reliability Engineering & System Safety, vol. 157, pp. 54–63, 2017. https://doi.org/10.1016/j.ress.2016.08.009
[14] V. Arunachalam, A. Calvache, and A. Tansu, “Some useful approximations for the availability function,” International Journal of Reliability, Quality and Safety Engineering, vol. 22, no. 2, p. 1550008 (15 pages), 2015. https://doi.org/10.1142/S0218539315500084
[15] L. Bednara, “Methods for approximating the availability functions,” Master’s
thesis, Delft University of Technologyy, Netherlands, 2008.
[16] A. Calvache, “Aproximaciones de las funciones de renovación y de disponibilidad, con aplicaciones en el área administrativa,” in XXIV Simposio Internacional de Estadística., 2014.
[17] A. Calvache, “The transient and asymptotic moments for the random mission time of a system,” Ciencia en Desarrollo, vol. 7, no. 2, pp. 109–124, 2016. https://doi.org/10.19053/01217488.v7.n2.2016.4917
[18] L. Cui, J. Chen, and B. Wu, “New interval availability indexes for markov repairable systems,” Reliability Engineering & System Safety, vol. 168, Mar. 2017. https://doi.org/10.1016/j.ress.2017.03.016
[19] B. Sericola, “Interval-availability distribution of 2-state systems with exponential failures and phase-type repairs,” IEEE Transactions on Reliability, vol. 43, no. 2, pp. 335–343, 1994. http://dx.doi.org/10.1109/24.295019
[20] L. Hu, D. Yue, and D. Zhao, “Availability equivalence analysis of a repairable series-parallel system,” Mathematical Problems in Engineering, vol. 2012, p. 15, 2012. http://dx.doi.org/10.1155/2012/957537
[21] A. Csenki, “A new approach to the cumulative operational time for semimarkov models of repairable systems,” Reliability Engineering and System Safety, vol. 54, pp. 11–21, 1996. https://doi.org/10.1016/S0951-8320(96)00065-8
[22] M. A. El-Damcese, A. N. Salem, and N. Temraz, “Semi-markov model of a series-parallel system subject to preventive maintenance,” Journal of Statistics Applications & Probability, vol. 3, pp. 307–318, 2013.
[23] L. R. Figueredo, “Planteamiento y solución de un sistema de ecuaciones integrales que modelan la disponibilidad de un sistema reparable.” Master’s thesis, Universidad de EAFIT, 2016.
[24] T. Boehme, W. Preuss, and V. Wall, “On a simple numerical method for computing stieltjes integrals in reliability theory,” Probability in the Engineering and Informational Sciences, vol. 5, no. 01, pp. 113–128, 1991. https://doi.org/10.1017/S0269964800001935
Article Sidebar
Article Details
Liliana Rodríguez-Figueredo, Universidad Pedagógica y Tecnológica de Colombia
Magíster en Matemáticas Aplicadas
Authors who publish with this journal agree to the following terms:
- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See The Effect of Open Access).