A High-Order HDG Method with Dubiner Basis for Elliptic Flow Problems
Main Article Content
Keywords
Hybridizable discontinuous Galerkin methods, flow in porous media, Dubiner’s basis, high order convergence
Abstract
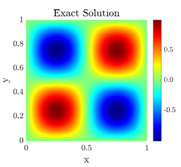
We propose a standard hybridizable discontinuous Galerkin (HDG) method to solve a classic problem in fluids mechanics: Darcy’s law. This model describes the behavior of a fluid trough a porous medium and it is relevant to the flow patterns on the macro scale. Here we present the theoretical results of existence and uniqueness of the weak and discontinuous solution of the second order elliptic equation, as well as the predicted convergence order of the HDG method. We highlight the use and implementation of Dubiner polynomial basis functions that allow us to develop a general and efficient high order numerical approximation. We also show some numerical examples that validate the theoretical results.
Downloads
References
[2] V. P. Singh, Kinematic wave modeling in water resources: Environmental hydrology. John Wiley & Sons, 1997.
[3] L. Rybach and L. J. P. Muffler, “Geothermal systems: principles and case histories,”wi, 1981.
[4] R. Helmig et al., Multiphase flow and transport processes in the subsurface: a contribution to the modeling of hydrosystems. Springer-Verlag, 1997.
[5] A. Atangana, Fractional operators with constant and variable order with application to geo-hydrology. Academic Press, 2017.
[6] J. E. Warren, H. S. Price et al., “Flow in heterogeneous porous media,” Society of Petroleum Engineers Journal, vol. 1, no. 03, pp. 153–169, 1961. https://doi.org/10.2118/1579-g
[7] R. Ababou, D. McLaughlin, L. W. Gelhar, and A. F. B. Tompson, “Numerical simulation of three-dimensional saturated flow in randomly heterogeneous porous media,” Transport in porous media, vol. 4, no. 6, pp. 549–565, 1989. https://doi.org/10.1007/bf00223627
[8] L. Bergamaschi, S. Mantica, and F. Saleri, “Mixed finite element approximation of Darcy’s law in porous media,” Report CRS4 AppMath-94-20, CRS4, Cagliari, Italy, 1994.
[9] F. Bassi and S. Rebay, “A high-order accurate discontinuous finite element method for the numerical solution of the compressible Navier-Stokes equations,” Journal of computational physics, vol. 131, no. 2, pp. 267–279, 1997. https://doi.org/10.1006/jcph.1996.5572
[10] B. Q. Li, Discontinuous finite elements in fluid dynamics and heat transfer. Springer Science & Business Media, 2005.
[11] B. Rivière and I. Yotov, “Locally conservative coupling of stokes and darcy flows,” SIAM Journal on Numerical Analysis, vol. 42, no. 5, pp. 1959–1977, 2005. https://doi.org/10.1137/s0036142903427640
[12] M. F. Wheeler, S. Sun, O. Eslinger, and B. Riviere, “Discontinuous galerkin method for modeling flow and reactive transport in porous media,” in Analysis and Simulation of Multifield Problems. Springer, 2003, pp. 37–56.
https://doi.org/10.1007/978-3-540-36527-3_3
[13] P. Bastian, “A fully-coupled discontinuous galerkin method for two-phase flow in porous media with discontinuous capillary pressure,” Computational Geosciences, vol. 18, no. 5, pp. 779–796, 2014. https://doi.org/10.1007/s10596-014-9426-y
[14] P. Bastian and B. Rivière, “Superconvergence and h (div) projection for discontinuous galerkin methods,” International journal for numerical methods in fluids, vol. 42, no. 10, pp. 1043–1057, 2003. https://doi.org/10.1002/fld.562
[15] S. Karpinski, I. S. Pop, and F. A. Radu, “Analysis of a linearization scheme for an interior penalty discontinuous galerkin method for two-phase flow in porous media with dynamic capillarity effects,” International Journal for Numerical Methods in Engineering, vol. 112, no. 6, pp. 553–577, 2017. https://doi.org/10.1002/nme.5526
[16] B. Cockburn, “The hybridizable discontinuous Galerkin methods,” in Proceedings of the International Congress of Mathematicians, vol. 4, 2014, pp. 2749–2775.
[17] B. Cockburn, J. Gopalakrishnan, and R. Lazarov, “Unified hybridization of discontinuous Galerkin, mixed, and continuous Galerkin methods for second order elliptic problems,” SIAM Journal on Numerical Analysis, vol. 47, no. 2, pp. 1319–1365, 2009. https://doi.org/10.1137/070706616
[18] A. Jaust and J. Schütz, “A temporally adaptive hybridized discontinuous Galerkin method for time-dependent compressible flows,” Computers & Fluids, vol. 98, pp. 177–185, 2014. https://doi.org/10.1016/j.compfluid.2014.01.019
[19] G. N. Gatica and F. A. Sequeira, “Analysis of an augmented HDG method for a class of quasi-newtonian Stokes flows,” Journal of Scientific Computing, vol. 65, no. 3, pp. 1270–1308, 2015. https://doi.org/10.1007/s10915-015-0008-5
[20] B. Cockburn and K. Shi, “Devising HDG methods for Stokes flow: An overview,” Computers & Fluids, vol. 98, pp. 221–229, 2014. https://doi.org/10.1016/j.compfluid.2013.11.017
[21] H. Egger and C. Waluga, “hp analysis of a hybrid DG method for Stokes flow,” IMA Journal of Numerical Analysis, p. drs018, 2012. https://doi.org/10.1093/imanum/drs018
[22] H. Egger and C. Waluga, “A hybrid discontinuous Galerkin method for Darcy-Stokes problems,” in
Domain decomposition methods in science and engineering XX. Springer, 2013, pp. 663–670. https://doi.org/10.1007/978-3-642-35275-1_79
[23] M. Dubiner, “Spectral methods on triangles and other domains,” J Sci Comput, vol. 6, no. 4, pp. 345–390, Dec. 1991. https://doi.org/10.1007/BF01060030
[24] S. Deng and W. Cai, “Analysis and application of an orthogonal nodal basis on triangles for discontinuous spectral element methods,” Applied Numerical Analysis & Computational Mathematics, vol. 2, no. 3, pp. 326–345, 2005. https://doi.org/10.1002/anac.200510007
[25] B. Cockburn, J. Gopalakrishnan, and F.-J. Sayas, “A projection-based error analysis of HDG methods,” Mathematics of Computation, vol. 79, no. 271, pp. 1351–1367, 2010. https://doi.org/10.1090/s0025-5718-10-02334-3
[26] B. Cockburn and B. Dong, “An analysis of the minimal dissipation local discontinuous Galerkin method for convection–diffusion problems,” Journal of Scientific Computing, vol. 32, no. 2, pp. 233–262, 2007. https://doi.org/10.1007/s10915-007-9130-3
[27] M. Abramowitz and I. A. Stegun, Handbook of mathematical functions: with formulas, graphs, and mathematical tables. Courier Corporation, 1964, vol. 55. https://doi.org/10.2307/1266136
[28] R. Pasquetti and F. Rapetti, “Spectral element methods on triangles and quadrilaterals: comparisons and applications,” Journal of Computational Physics, vol. 198, no. 1, Jul. 2004. https://doi.org/10.1016/j.jcp.2004.01.010
[29] Z. Fu, L. F. Gatica, and F.-J. Sayas, “Matlab tools for HDG in three dimensions,” arXiv preprint arXiv:1305.1489, 2013.