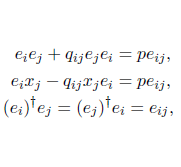e— Cálculo
Main Article Content
Keywords
e— derivada, e— álgebra, e— integral, q — e álgebra
Resumen
En este trabajo se formula el e— cálculo en base a la naturaleza de las cargas eléctricas, usando la tercera ley de Newton y la ley de Coulomb, la e— álgebra y la q — e álgebra deformada, asociando las variables ei; ej como cargas elementales, y x como la variable conductora. Se define la e— derivada a partir de un simple experimento de encendido y apagado de un bombillo respectivamente. Por otro lado, se formulan las e— series, la e— integral, las q — e derivadas, series e integrales y sus respectivos criterios de convergencia. Sobre las e— integrales se establecen un camino o contorno cerrado Γ (x) para definir las e— integrales de contorno, y finalmente se formulan el q — e cálculo deformado y la q — e álgebra de Heisenberg.
Descargas
Referencias
[2] C. A. Coulomb, Premier-[troisième] mémoire sur l’electricité et le magnétisme. Académie Royale des sciences, 1785.
[3] W. R. Hamilton, “On quaternions; or on a new system of imaginaries in algebra,” Philosophical magazine, vol. 25, no. 3, pp. 489–495, 1844. https://www.emis.de/classics/Hamilton/OnQuat.pdf
[4] H. Grassmann, Die lineale Ausdehnungslehre ein neuer Zweig der Mathematik: dargestellt und durch Anwendungen auf die übrigen Zweige der Mathematik, wie auch auf die Statik, Mechanik, die Lehre vom Magnetismus und die Krystallonomie erläutert. O. Wigand, 1844, vol. 1.
[5] F. H. Jackson, “Xi.—on q-functions and a certain difference operator,” Earth and Environmental Science Transactions of the Royal Society of Edinburgh, vol. 46, no. 2, pp. 253–281, 1909. https://doi.org/10.1017/ S0080456800002751
[6] W. Heisenberg, “Über quantentheoretische umdeutung kinematischer und mechanischer beziehungen,” in Original Scientific Papers Wissenschaftliche Originalarbeiten. Springer, 1985, pp. 382–396. https://doi.org/10.1007/BF01328377
[7] H. Weyl, “Gruppentheorie und quantenmechanik,” Zeitschrift für Physik, no. 46, pp. 1–46, 1928. https://doi.org/10.1007/BF02055756
[8] L. Hellstrom and S. Silvestrov, Commuting elements in q-deformed Heisenberg algebras. World Scientific, 2000.
[9] C. Walton, “An invitation to noncommutative algebra,” in A Celebration of the EDGE Program’s Impact on the Mathematics Community and Beyond. Springer, 2019, pp. 339–366. https://arxiv.org/pdf/1808.03172.pdf
[10] A. Reyes and J. Jaramillo, “Symmetry and reversibility properties for quantum algebras and skew poincaré birkhoff-witt extensions,” Ingeniería y Ciencia, vol. 14, no. 27, pp. 29–52, 2018. https://doi.org/10.17230/ ingciencia.14.27.2
[11] S. A. Lopes and F. Razavinia, “Quantum generalized heisenberg algebras and their representations,” arXiv preprint arXiv:2004.09301, 2020. https://arxiv.org/pdf/2004.09301.pdf
[12] M. Tuval and A. Yahalom, “Newton’s third law in the framework of special relativity,” The European Physical Journal Plus, vol. 129, no. 11, pp. 1–8, 2014. https://arxiv.org/pdf/1302.2537v1.pdf
[13] F. B. Kneubil, “Breaking newton’s third law: electromagnetic instances,” European Journal of Physics, vol. 37, no. 6, p. 065201, 2016. https: //doi.org/10.1088/0143-0807/37/6/065201
[14] V. Kac, “Ch. pokman,” Quantum Calculus, Springer–Verlag, New York, 2002.
[15] V. V. Zharinov, “On derivations of the heisenberg algebra,” Theoretical and mathematical physics, vol. 118, no. 2, pp. 129–151, 1999. https: //doi.org/10.1007/BF02557307
[16] B. J. Rana, R. Ahmed, and S. Ahmmed, “Effects of variable electrical conductivity and thermal conductivity on unsteady mhd free convection flow past an exponential accelerated inclined plate,” in AIP Conference Proceedings, vol. 1851, no. 1. AIP Publishing LLC, 2017, p. 020058. https://doi.org/10.1063/1.4984687