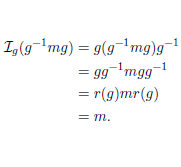The Notions of Center, Commutator and Inner Isomorphism for Groupoids
Main Article Content
Keywords
Groupoid, normal subgroupoid, normalizer, center, commutator, inner isomorphisms
Abstract
In this paper we introduce some algebraic properties of subgroupoids and normal subgroupoids. we define other things, we define the normalizer of a wide subgroupoid H of a groupoid G and show that, as in the case of groups, this normalizer is the greatest wide subgroupoid of G in which H is normal. Furthermore, we provide definitions of the center Z(G) and the commutator G' of the groupoid G and prove that both of them are normal subgroupoids. We give the notions of inner and partial isomorphism of G and show that the groupoid I(G) given by the set of all the inner isomorphisms of G is a normal subgroupoid of A(G), the set of all the partial isomorphisms of G. Moreover, we prove that I(G) is isomorphic to the quotient groupoid G/Z(G), which extends to groupoids the corresponding well-known result for groups.
Downloads
References
[1] H. Brandt, “Über eine verallgemeinerung des gruppenbegriffes,” Math. Ann, vol. 96, pp. 360–366, 1926.
[2] C. Ehresmann, OEuvres complètes et commentées, ser. Oeuvres complétes. Topologie algéBrique et géométrie différentielle, 1950, no. partes 1-2.
[3] R. Brown, “From groups to groupoids: a brief survey,” Bulletin of The London Mathematical Society - BULL LOND MATH SOC, vol. 19, pp. 113–134, 03 1987. https://doi.org/10.1112/blms/19.2.113
[4] A. Ibort and M. Rodríguez, “On the structure of finite groupoids and their representations,” Symmetry, vol. 11, p. 414, 03 2019. https://doi.org/10.3390/sym11030414
[5] G. Ivan, “Strong morphisms of groupoids,” Balk. J. Geom. Appl., vol. 1, no. 4, pp. 91–102, 1999. https://www.emis.de/journals/BJGA/v04n1/B04-1-IVAN.pdf
[6] G. Ivan, “Algebraic constructions of brandt groupoids,” pp. 69–90, 01 2002.
[7] S. Zakrzewski, “Quantum and classical pseudogroups. ii. differential and symplectic pseudogroups,” Comm. Math. Phys., vol. 134, no. 2, pp. 371–395, 1990. https://projecteuclid.org:443/euclid.cmp/1104201735
[8] P. Stachura, “Short and biased introduction to groupoids,” J. Knot Theor. Ramif., vol. 27, no. 7, pp. 1–13, 2018. https://arxiv.org/pdf/1311.3866.pdf
[9] M. Lawson, Inverse Semigroups: The Theory of Partial Symmetries. World Scientific, 1998. https://books.google.com.co/books?id=2805q4tFiCkC
[10] A. Paques and T. Tamusiunas, “The galois correspondence theorem for groupoid actions,” Journal of Algebra, vol. 509, pp. 105 – 123, 2018. https://doi.org/10.1016/j.jalgebra.2018.04.034
[11] J. Ávila, V. Marín, and H. Pinedo, “Isomorphism theorems for groupoids and some applications,” Int. J. Math. Math. Sci., vol. 2020, no. 3967368, pp. 1–10, 2020. https//doi.org/10.1155/2020/3967368
[12] B. Bainson and N. D. Gilbert, “The homology of principally directed ordered groupoids,” Homology Homotopy Appl., vol. 22, no. 1, pp. 1–9, 2019. https://arxiv.org/pdf/1704.03689v1.pdf
[13] H. Myrnouri and M. Amini, “Decomposable abelian groupoids,” Int. Math. Forum, vol. 5, no. 48, pp. 2371–2380, 2010.
[14] D. S. Dummit and R. M. Foote, Abstract Algebra, 3rd ed. New Delhi: Wiley, june 2003.
Article Sidebar
Article Details
Jesús Ávila, Universidad del Tolima
Departamento de Matemáticas y Estadística
Universidad del Tolima
Víctor Marín, Universidad del Tolima
Profesor del Departamento de Matemáticas y Estadística de la Universidad del Tolima. Doctor en Matemáticas de la Universidad Federal de Rio Grande Do Sul.
Authors who publish with this journal agree to the following terms:
- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See The Effect of Open Access).