Un esquema de elementos finitos completamente discreto para la ecuación de Derrida-Lebowitz-Speer-Spohn
Main Article Content
Keywords
Elementos finitos, Ecuaciones no lineales de evolución, Semiconductores.
Resumen
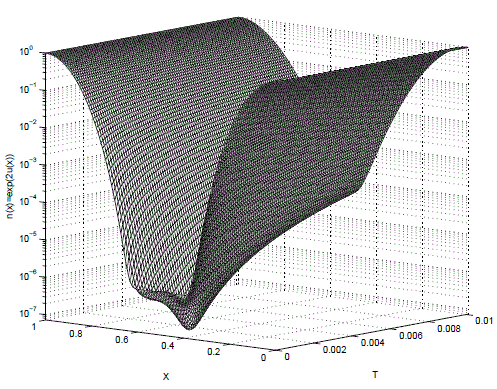
La ecuación de Derrida-Lebowitz-Speer-Spohn (DLSS) es una ecuación de evolución no lineal de cuarto orden. Esta aparece en el estudio de las fluctuaciones de interface de sistemas de espín y en la modelación de semicoductores cuánticos. En este artículo, se presenta una discretización por elementos finitos para una formulación exponencial de la ecuación DLSS abordada como un sistema acoplado de ecuaciones. Usando la información disponible acerca del fenómeno físico, se establecen las condiciones de contorno para el sistema acoplado. Se demuestra la existencia de la solución discreta global en el tiempo via un argumento de punto fijo. Los resultados numéricos ilustran el carácter cuántico de la ecuación. Finalmente se presenta un test del orden de convergencia de la discretización porpuesta.
MSC: 35G25, 65M60, 82D37
Descargas
Referencias
[2] B. Derrida, J. L. Lebowitz, E. R. Speer, and H. Spohn, “Fluctuations of a stationary nonequilibrium interface,” Phys. Rev. Lett., vol. 67, pp. 165–168, July 1991. 98
[3] R. Pinnau, “The Linearized Transient Quantum Drift Diffusion Model-Stability of Stationary States,” ZAMM - Journal of Applied Mathematics and Mechanics / Zeitschrift für Angewandte Mathematik und Mechanik, vol. 80, no. 5, pp. 327–344, 2000. 98, 101
[4] L. L. A. Peletier and W. C. Troy, Spatial Patterns: Higher Order Models in Physics and Mechanics. Progress in Nonlinear Differential Equations and Their Applications Series, Boston: Springer, 2001. 99
[5] A. Jüngel and R. Pinnau, “Global Non-Negative Solutions of a Nonlinear Fourth-Order Parabolic Equation for Quantum Systems,” 2000. 99, 100, 108
[6] A. Jüngel and D. Matthes, “The Derrida-Lebowitz-Speer-Spohn equation: Existence, NonUniqueness, and Decay Rates of the Solutions,” SIAM Journal on Mathematical Analysis, vol. 39, no. 6, pp. 1996–2015, 2008. 99
[7] M. J. Cáceres, J. A. Carrillo, and G. Toscani, “Long-Time Behavior for a Nonlinear Fourth-Order Parabolic Equation,” Transactions of the American Mathematical Society, vol. 357, no. 3, pp. 1161–1175, 2005. 99
[8] M. Pia Gualdani, A. Jüngel, and G. Toscani, “A Nonlinear Fourth order Parabolic Equation with Nonhomogeneous Boundary Conditions,” SIAM Journal on Mathematical Analysis, vol. 37, no. 6, pp. 1761–1779, 2006. 99
[9] A. Jüngel and G. Toscani, “Exponential time decay of solutions to a nonlinear fourth-order parabolic equation,” Zeitschrift für angewandte Mathematik und Physik ZAMP, vol. 54, no. 3, pp. 377–386, 2003. 99
[10] B. Düring, D. Matthes, and J. P. Milišić, “A gradient flow scheme for nonlinear fourth order equations,” Discrete and Continuous Dynamical Systems - Series B (DCDS-B), vol. 14, no. 3, pp. 935 – 959, 2010. 99, 108
[11] R. Pinnau, “A note on boundary conditions for quantum hydrodynamic equations,” Applied Mathematics Letters, vol. 12, no. 5, pp. 77–82, 1999. 101
[12] M. G. Ancona and H. F. Tiersten, “Macroscopic physics of the silicon inversion layer,” Phys. Rev. B, vol. 35, pp. 7959–7965, May 1987. 101
[13] E. Zeidler, Nonlinear Functional Analysis and Its Applications II/A. Berlin: Springer-Verlag, 1 ed., 1990. 106
Article Sidebar
Article Details
Los autores que publican en esta revista están de acuerdo con los siguientes términos:
- Los autores conservan los derechos de autor y garantizan a la revista el derecho de ser la primera publicación del trabajo al igual que licenciado bajo una Creative Commons Attribution License que permite a otros compartir el trabajo con un reconocimiento de la autoría del trabajo y la publicación inicial en esta revista.
- Los autores pueden establecer por separado acuerdos adicionales para la distribución no exclusiva de la versión de la obra publicada en la revista (por ejemplo, situarlo en un repositorio institucional o publicarlo en un libro), con un reconocimiento de su publicación inicial en esta revista.
- Se permite y se anima a los autores a difundir sus trabajos electrónicamente (por ejemplo, en repositorios institucionales o en su propio sitio web) antes y durante el proceso de envío, ya que puede dar lugar a intercambios productivos, así como a una citación más temprana y mayor de los trabajos publicados (Véase The Effect of Open Access) (en inglés).