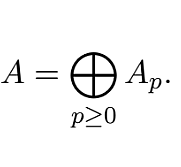Nakayama Automorphism of Some Skew PBW Extensions
Main Article Content
Keywords
Skew PBW extensions, Nakayama automorphism, Artin- Schelter regular algebras, Calabi-Yau algebras
Abstract
Let R be an Artin-Schelter regular algebra and A = σ(R)⟨x1,...,xn⟩ a graded quasi-commutative skew PBW extension over R. In this paper we describe the Nakayama automorphism of A using the Nakayama automor- phism of the ring of coefficients R. We calculate explicitly the Nakayama automorphism of some skew PBW extensions.
Downloads
Download data is not yet available.
References
[1] M. Reyes, D. Rogalski, and J. J. Zhang, “Skew Calabi-Yau algebras and homological identities,” Adv. in Math., vol. 264, pp. 308–354, 2014.
[2] L.-Y. Liu, S. Wang, and Q.-S. Wu, “Twisted Calabi-Yau property of Ore extensions,” J. Noncommut. Geom., vol. 8, no. 2, pp. 587–609, 2014.
[3] J.-F. Lü, X.-F. Mao, and J. Zhang, “Nakayama automorphism and applications,” Tran. Amer. Math. Soc., vol. 369, pp. 2425–2460, 2017. [Online]. Available: https://doi.org/10.1090/tran/6718
[4] J.-F. Lü, X.-F. Mao, and J. J. Zhang, “The nakayama automorphism of a class of graded algebras,” Israel Journal of Mathematics, vol. 219, no. 2, pp. 707–725, Apr 2017. [Online]. Available: https: //doi.org/10.1007/s11856-017-1495-x
[5] Y. Shen, G.-S. Zhou, and D.-M. Lu, “Nakayama automorphisms of twisted tensor products,” Journal of Algebra, vol. 504, no. 15, pp. 445 – 478, 2018. [Online]. Available: https://doi.org/10.1016/j.jalgebra.2018.02.025
[6] Y. Liu and W. Ma, “Nakayama automorphism of Ore extensions over polynomial algebras,” arXiv:1808.03589v1 [math.RA], pp. 1–12, 2018.
[7] C. Gallego and O. Lezama, “Gröbner bases for ideals of σ-PBW extensions,” Comm. Algebra, vol. 39, no. 1, pp. 50–75, 2011.
[8] O. Lezama and A. Reyes, “Some homological properties of skew PBW extensions,” Comm. Algebra, vol. 42, pp. 1200–1230, 2014.
[9] H. Suárez, “Koszulity for graded skew PBW extensions,” Communications in Algebra, vol. 45, no. 10, pp. 4569–4580, 2017. [Online]. Available: https://doi.org/10.1080/00927872.2016.1272694
[10] H. Suárez, “N-Koszul algebras, Calabi-Yau algebras and skew PBW extensions,” Ph.D. Thesis, Universidad Nacional de Colombia, sede Bogotá, 2017.
[11] A. Reyes and J. Jaramillo, “Symmetry and reversibility properties for quantum algebras and skew Poincaré-Birkhoff-Witt extensions,” Ingenieria y Ciencia, vol. 14, no. 27, pp. 29–52, 2018. [Online]. Available: https://doi.org/10.17230/ingciencia.14.27.2
[12] A. Reyes and H. Suárez, “Enveloping algebra and Calabi-Yau algebras over skew Poincaré-Birkhoff-Witt extensions,” Far East J. Math. Sci. (FJMS), vol. 102, no. 2, pp. 373–397, 2017.
[13] A. Reyes and H. Suárez, “A notion of compatibility for Armendariz and baer properties over skew PBW extensions,” Revista de la Unión Matemática Argentina, vol. 59, no. 1, pp. 157–178, 10 2017. [Online]. Available: https://doi.org/10.33044/revuma.v59n1a08
[14] ——, “σ-PBW extensions of skew Armendariz rings,” Advances in Applied Clifford Algebras, vol. 27, pp. 3197–3224, 11 2016. [Online]. Available: https://doi.org/10.1007/s00006-017-0800-4
[15] H. Suárez and A. Reyes, “Koszulity for skew pbw extensions over fields,” JP Journal of Algebra, Number Theory and Applications, 39 (2), 2017, 181-203. [Online]. Available: https://doi.org/10.17654/NT039020181
[16] A. Reyes and H. Suárez, “Some remarks about the cyclic homology of skew PBW extensions,” Ciencia en Desarrollo, vol. 7, no. 2, pp. 99–107, 2016.
[17] H. Suárez, O. Lezama, and A. Reyes, “Calabi-Yau property for graded skew PBW extensions,” Rev. Colombiana Mat., vol. 51, no. 2, pp. 221–238, 2017.
[18] D. Rogalski, Noncommutative projective geometry. In Noncommutative algebraic geometry. vol. 64 of Math. Sci. Res. Inst. Publ., 13-70, 64th ed. New York: Cambridge Univ. Press, 2016.
[19] J. Goodman and U. Krähmer, “Untwisting a twisted Calabi-Yau algebra,” J. Algebra, vol. 406, pp. 271–289, 2014.
[20] R. Berger and R. Taillefer, “Poincaré-Birkhoff-Witt deformations of CalabiYau algebras,” J. Noncommut. Geom., vol. 1, pp. 241–270, 2007.
[21] K. R. Goodearl and R. B. Warfield, An Introduction to Noncommutative Noetherian Rings, 2nd ed. London: London Mathematical Society Student Texts, 2004.
[22] J. Gómez and H. Suárez, “Algunas propiedades homológicas del plano de Jordan,” Ciencia en Desarrollo, vol. 9, no. 2, pp. 67–80, 2018.
[23] R. Berger, “Gerasimov’s theorem and N-Koszul algebras,” J. London Math. Soc., vol. 79, pp. 631–648, 2009.
[24] C. Zhu, F. V. Oystaeyen, and Y. Zhang, “Nakayama automorphism of double Ore extensions of Koszul regular algebras,” Manuscripta math., vol. 152, no. 3-4, pp. 555–584, 2017.
[2] L.-Y. Liu, S. Wang, and Q.-S. Wu, “Twisted Calabi-Yau property of Ore extensions,” J. Noncommut. Geom., vol. 8, no. 2, pp. 587–609, 2014.
[3] J.-F. Lü, X.-F. Mao, and J. Zhang, “Nakayama automorphism and applications,” Tran. Amer. Math. Soc., vol. 369, pp. 2425–2460, 2017. [Online]. Available: https://doi.org/10.1090/tran/6718
[4] J.-F. Lü, X.-F. Mao, and J. J. Zhang, “The nakayama automorphism of a class of graded algebras,” Israel Journal of Mathematics, vol. 219, no. 2, pp. 707–725, Apr 2017. [Online]. Available: https: //doi.org/10.1007/s11856-017-1495-x
[5] Y. Shen, G.-S. Zhou, and D.-M. Lu, “Nakayama automorphisms of twisted tensor products,” Journal of Algebra, vol. 504, no. 15, pp. 445 – 478, 2018. [Online]. Available: https://doi.org/10.1016/j.jalgebra.2018.02.025
[6] Y. Liu and W. Ma, “Nakayama automorphism of Ore extensions over polynomial algebras,” arXiv:1808.03589v1 [math.RA], pp. 1–12, 2018.
[7] C. Gallego and O. Lezama, “Gröbner bases for ideals of σ-PBW extensions,” Comm. Algebra, vol. 39, no. 1, pp. 50–75, 2011.
[8] O. Lezama and A. Reyes, “Some homological properties of skew PBW extensions,” Comm. Algebra, vol. 42, pp. 1200–1230, 2014.
[9] H. Suárez, “Koszulity for graded skew PBW extensions,” Communications in Algebra, vol. 45, no. 10, pp. 4569–4580, 2017. [Online]. Available: https://doi.org/10.1080/00927872.2016.1272694
[10] H. Suárez, “N-Koszul algebras, Calabi-Yau algebras and skew PBW extensions,” Ph.D. Thesis, Universidad Nacional de Colombia, sede Bogotá, 2017.
[11] A. Reyes and J. Jaramillo, “Symmetry and reversibility properties for quantum algebras and skew Poincaré-Birkhoff-Witt extensions,” Ingenieria y Ciencia, vol. 14, no. 27, pp. 29–52, 2018. [Online]. Available: https://doi.org/10.17230/ingciencia.14.27.2
[12] A. Reyes and H. Suárez, “Enveloping algebra and Calabi-Yau algebras over skew Poincaré-Birkhoff-Witt extensions,” Far East J. Math. Sci. (FJMS), vol. 102, no. 2, pp. 373–397, 2017.
[13] A. Reyes and H. Suárez, “A notion of compatibility for Armendariz and baer properties over skew PBW extensions,” Revista de la Unión Matemática Argentina, vol. 59, no. 1, pp. 157–178, 10 2017. [Online]. Available: https://doi.org/10.33044/revuma.v59n1a08
[14] ——, “σ-PBW extensions of skew Armendariz rings,” Advances in Applied Clifford Algebras, vol. 27, pp. 3197–3224, 11 2016. [Online]. Available: https://doi.org/10.1007/s00006-017-0800-4
[15] H. Suárez and A. Reyes, “Koszulity for skew pbw extensions over fields,” JP Journal of Algebra, Number Theory and Applications, 39 (2), 2017, 181-203. [Online]. Available: https://doi.org/10.17654/NT039020181
[16] A. Reyes and H. Suárez, “Some remarks about the cyclic homology of skew PBW extensions,” Ciencia en Desarrollo, vol. 7, no. 2, pp. 99–107, 2016.
[17] H. Suárez, O. Lezama, and A. Reyes, “Calabi-Yau property for graded skew PBW extensions,” Rev. Colombiana Mat., vol. 51, no. 2, pp. 221–238, 2017.
[18] D. Rogalski, Noncommutative projective geometry. In Noncommutative algebraic geometry. vol. 64 of Math. Sci. Res. Inst. Publ., 13-70, 64th ed. New York: Cambridge Univ. Press, 2016.
[19] J. Goodman and U. Krähmer, “Untwisting a twisted Calabi-Yau algebra,” J. Algebra, vol. 406, pp. 271–289, 2014.
[20] R. Berger and R. Taillefer, “Poincaré-Birkhoff-Witt deformations of CalabiYau algebras,” J. Noncommut. Geom., vol. 1, pp. 241–270, 2007.
[21] K. R. Goodearl and R. B. Warfield, An Introduction to Noncommutative Noetherian Rings, 2nd ed. London: London Mathematical Society Student Texts, 2004.
[22] J. Gómez and H. Suárez, “Algunas propiedades homológicas del plano de Jordan,” Ciencia en Desarrollo, vol. 9, no. 2, pp. 67–80, 2018.
[23] R. Berger, “Gerasimov’s theorem and N-Koszul algebras,” J. London Math. Soc., vol. 79, pp. 631–648, 2009.
[24] C. Zhu, F. V. Oystaeyen, and Y. Zhang, “Nakayama automorphism of double Ore extensions of Koszul regular algebras,” Manuscripta math., vol. 152, no. 3-4, pp. 555–584, 2017.
Article Sidebar
Published
May 31, 2019
Article Details
How to Cite
Suárez, H., & Reyes, A. (2019). Nakayama Automorphism of Some Skew PBW Extensions. Ingeniería Y Ciencia, 15(29), 157–177. https://doi.org/10.17230/ingciencia.15.29.6
Issue
Section
Articles
Supporting Agencies
Universidad Nacional de Colombia
Author Biographies
Héctor Suárez, Universidad Pedagógica y Tecnológica de Colombia
Profesor de la Escuela de matemáticas y estadística.
Armando Reyes, Universidad Nacional de Colombia
Doctor en Ciencias Matemáticas, profesor del Departamento de Matemáticas.
Authors who publish with this journal agree to the following terms:
- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See The Effect of Open Access).