Determinants of New Housing Prices in Bogotá for 2019: an Approach Through a Semiparametric Spatial Regression Model
Main Article Content
Keywords
Hedonic models, spatial econometrics, housing price, semiparametric regression
Abstract
This document uses the recent advances in the field of spatial econometrics to develop a semi-parametric regression model that allows the inclusion of non-linearities and the modeling of spatial heterogeneity through a
two-dimensional function that depends on geographic coordinates. The methodology is applied in a hedonic model for the price of new housing in Bogotá where a remarkable fit is obtained, in terms of the mean square
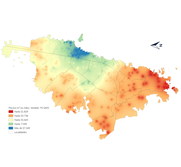
error and the R2. The empirical result shows that the housing delivery condition, stratum, and construction state affect the price in a linear way, while the area, and the distances to parks, roads and Transmilenio stations present non-linear results, additionaly, it was possible to model the spatial trend that represents the location on the value of the house where an increase is appreciated towards the northeast of the city. Thus, it is concluded that the estimated model allows the relationship between the explanatory variables and the dependent variable to be measured flexibly, establishing itself as a good alternative to understand the formation of prices in the real estate market.
Downloads
References
[2] D. Desormeaux and F. Piguillem, “Precios hedónicos e índices de precios de viviendas,” Documento de trabajo, no. 12, 2003.
[3] L. Anselin, Spatial econometrics: methods and models. Springer Science & Business Media, 1988, vol. 4.
[4] R. M. Serrano and E. V. Valcarce, Técnicas econométricas para el tratamiento de datos espaciales: la econometría espacial. Edicions Universitat Barcelona, 2000, vol. 44.
[5] C. Chasco Yrigoyen, “Modelos de heterogeneidad espacial,” University Library of Munich, Germany, Tech. Rep., 2004. https://www.researchgate.net/publication/23742953_Modelos_de_heterogeneidad_espacial
[6] J. Montero, R. Mínguez, and M. Durbán, “Sar models with nonparametric spatial trends. a p-spline approach,” Estadística Española, vol. 54, no. 177, pp. 89–111, 2012.
[7] R. Basile and R. Mínguez, “Advances in spatial econometrics: Parametric vs. semiparametric spatial autoregressive models,” The economy as a complex spatial system, pp. 81–106, 2018. https://doi.org/10.1007/978-3-319-65627-4_4
[8] CAMACOL, “Estudio de oferta y demanda de vivienda y no habitacionales en Bogotá y Cundinamarca,” Tech. Rep., 2019. https://ww2.camacolcundinamarca.co/documentos/EstudiosEspecificos/LAE-CAMACOL2019.pdf
[9] K. J. Lancaster, “A new approach to consumer theory,” Journal of political economy, vol. 74, no. 2, pp. 132–157, 1966. https://doi.org/10.1086/259131
[10] S. Rosen, “Hedonic prices and implicit markets: product differentiation in pure competition,” Journal of political economy, vol. 82, no. 1, pp. 34–55, 1974. https://doi.org/10.1086/260169
[11] L. Anselin, “Spatial regression,” The SAGE handbook of spatial analysis, vol. 1, pp. 255–276, 2009.
[12] A. Sagner, “Determinantes del precio de viviendas en la región metropolitana de Chile,” El trimestre económico, vol. 78, no. 312, pp. 813–839, 2011. http://www.scielo.org.mx/pdf/ete/v78n312/2448-718X-ete-78-312-00813.pdf
[13] S. León, “Precios inmobiliarios en caba: un análisis econométrico espacial, desde lo global a lo local,” 2016. https://www.researchgate.net/publication/311641420_Precios_inmobiliarios_en_CABA_un_analisis_econometrico_espacial_desde_lo_global_a_lo_local
[14] J. I. Zoloa, “Tópicos en el mercado inmobiliario: un análisis desde la econometría espacial,” 2015. https://doi.org/10.35537/10915/49057
[15] L. Galvis, B. Carrillo et al., “índice de precios espacial para la vivienda urbana en Colombia: una aplicación con métodos de emparejamiento,” Revista de Economía del Rosario, vol. 16, no. 1, pp. 25–29, 2013. https://revistas.urosario.edu.co/index.php/economia/article/view/2829
[16] M. A. Urrea Zora, N. Cárdenas Mazo et al., “Un modelo espacial de precios hedónicos y calidad de vecindario: una aplicación para
Medellín, Colombia,” B.S. thesis, Universidad EAFIT, 2019. https://repository.eafit.edu.co/handle/10784/14941
[17] J. C. Duque, H. V. Ceballos, and J. Agudelo, “Infraestructura pública y precios de vivienda: una aplicación de regresión geográficamente ponderada en el contexto de precios hedónicos,” Ecos de Economía: A Latin American Journal of Applied Economics, vol. 15, no. 33, pp. 99–122, 2011.
[18] M. Rodríguez Gómez, “Caracterización hedónica del mercado de finca raíz en la ciudad de Cartagena: una aproximación semiparamétrica,” Economía y Región, vol. 1, no. 1, 2004. https://revistas.utb.edu.co/index.php/economiayregion/article/view/265
[19] C. Melo and O. Melo, “Estimación de precios hedónicos para propiedades residencial y comercial en la ciudad de Bogotá,” Ingeniería, vol. 8, no. 1, pp. 10–18, 2003.
[20] J. C. Mendieta, J. A. Perdomo et al., Especificación y estimación de un modelo de precios hedónico espacial para evaluar el impacto de Transmilenio sobre el valor de la propiedad en Bogotá. Univ. de los Andes, Fac. de Economía, CEDE Centro de Estudios sobre Desarrollo Económico, 2007. http://hdl.handle.net/1992/8115
[21] S. Higuera, “Modelación hedónico espacial de los determinantes del precio de la vivienda nueva en Bogotá,” Universidad Nacional de Colombia, Colombia, Tech. Rep., 2010.
[22] W. A. Cabrera-Rodríguez, J. S. Mariño-Montaña, and C. A. Quicazán-Moreno, “Modelos hedónicos con efectos espaciales: una
aproximación al cálculo de índices de precios de vivienda para Bogotá,” Borradores de Economía, no. 1072, 2019. https://doi.org/10.32468/be.1072
[23] R. Mínguez, M. L. Durbán, and R. Basile, “Spatio-temporal autoregressive semiparametric model for the analysis of regional economic data,” Stat. Methods Appl, vol. 16126, 2019.
[24] R. Mínguez, R. Basile, and M. Durbán, “An alternative semiparametric model for spatial panel data,” Statistical Methods & Applications, vol. 29, no. 4, pp. 669–708, 2020. https://doi.org/10.1007/s10260-019-00492-8
[25] J.-M. Montero, R. Mínguez, and G. Fernández-Avilés, “Housing price prediction: parametric versus semi-parametric spatial hedonic models,” Journal of Geographical Systems, vol. 20, no. 1, pp. 27–55, 2018. https://doi.org/10.1007/s10109-017-0257-y
[26] B. Manganelli, P. Pontrandolfi, A. Azzato, and B. Murgante, “Using geographically weighted regression for housing market segmentation,” International Journal of Business Intelligence and Data Mining 13, vol. 9, no. 2, pp. 161–177, 2014. https://doi.org/10.1504/IJBIDM.2014.065100
[27] G. Simpson, “Package gratia,” R package version, 2021.
[28] S. Wood, “Package mgcv,” R package version, 2020.
[29] S. N. Wood, Generalized additive models: an introduction with R. CRC press, 2017.
[30] P. H. Eilers, I. D. Currie, and M. Durbán, “Fast and compact smoothing on large multidimensional grids,” Computational Statistics & Data Analysis, vol. 50, no. 1, pp. 61–76, 2006. https://doi.org/10.1016/j.csda.2004.07.008
[31] M. X. Rodríguez-Álvarez, D.-J. Lee, T. Kneib, M. Durbán, and P. Eilers, “Fast smoothing parameter separation in multidimensional generalized p-splines: the sap algorithm,” Statistics and Computing, vol. 25, no. 5, pp. 941–957, 2015. https://doi.org/10.1007/s11222-014-9464-2
[32] J. Castaño, M. Laverde, M. Morales, and A. Yaruro, “Índice de precios de la vivienda nueva para Bogotá: metodología de precios hedónicos,” Temas de Estabilidad financiera, vol. 78, 2013.
[33] R. C. Team et al., “R: A language and environment for statistical computing,” 2020.
[34] R. Bivand, M. Altman, L. Anselin, R. Assunção, O. Berke, A. Bernat, and G. Blanchet, “Package spdep,” The Comprehensive R Archive Network, 2020. https://cran.r-project.org/web/packages/spdep/spdep.pdf
[35] R. Mínguez, R. Basile, and M. Durbán, “sptpsar: an R package for the development of semiparametric spatial and spatio-temporal econometric models,” Tech. Rep.
[36] R. Basile, M. Durbán, R. Mínguez, J. M. Montero, and J. Mur, “Modeling regional economic dynamics: Spatial dependence, spatial heterogeneity and nonlinearities,” Journal of Economic Dynamics and Control, vol. 48, pp. 229–245, 2014. https://doi.org/10.1016/j.jedc.2014.06.011
[37] J. Harezlak, D. Ruppert, and M. P. Wand, Semiparametric regression with R. Springer, 2018. https://link.springer.com/book/10.1007/978-1-4939-8853-2
[38] J. A. C. Rubio, F. J. C. Guzmán, and J. Otero, “Una base de datos de precios y características de vivienda en Colombia con información de internet,” Revista de economía del Rosario, vol. 22, no. 1, pp. 75–100, 2019. https://doi.org/10.12804/revistas.urosario.edu.co/economia/a.7768
[39] L. Wang, “Spatial econometric issues in hedonic property value models: model choice and endogenous land use,” Tech. Rep., 2006. https://etda.libraries.psu.edu/files/final_submissions/3844
[40] R. Cellmer, K. Kobylinska, and M. Bełej, “Application of hierarchical spatial autoregressive models to develop land value maps in urbanized areas,” ISPRS International Journal of Geo-Information, vol. 8, no. 4, p. 195, 2019. https://doi.org/10.3390/ijgi8040195