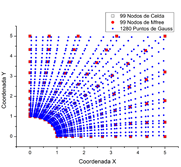
Solución del problema de Kirsch mediante elementos libres de malla, utilizando funciones de interpolación de base radial
Main Article Content
Keywords
Mfree, Mfree (Elementos Libres de Malla), Elementos Libres de Malla, RPIM (Método de interpolación de puntos radiales), RPIM, MQ (Multi-cuadráticas)., Método de Interpolación de Puntos Radiales, RBF, Funciones de Base Radial Multicuadráticas
Resumen
El problema de Kirsch publicado en 1898, es utilizado como base para corroborar la precisión relativa de los métodos numéricos desarrollados en la mecánica de sólidos. Por esta razón se utiliza la solución de este problema para evaluar la precisión del método numérico Mfree con una función de forma utilizando los puntos radiales de interpolación, en el método numérico libre de malla. El método de puntos radiales de interpolación es una técnica de interpolación utilizada para construir funciones de forma con nodos distribuidos localmente en una formulación débil la cual permite representar el problema como un sistema de ecuaciones. El tipo de funciones más usuales son las funciones polinomiales o funciones de base radial MQ (RBF, radio basis functions), la cual fue utilizada por la estabilidad que presenta al momento de solucionar el problema numéricamente. Para hacer la comparación se usó la solución analítica dada por Kirsch y la solución numérica desarrollada en el presente trabajo, obtenido un error del 0.00899% lo que muestra que la técnica Mfree con bases radiales de interpolación MQ son precisas y confiables al momento de ser utilizadas como método numérico de análisis.
Descargas
Referencias
[2] W. P. Jones, R. A. Frazer and S. W. Skan, “Approximations to functions and to the solutions of differential equations,” Britain Aerospace Research Council London. Report and Memo No. 1799. Reprinted in Great Britain Air Ministry Aerospace Research Communication Technical Report, 1, 735, Tech. Rep., 1937.
[3] C. Lanczos, “Trigonometric Interpolation of Empirical and Analytical Functions,” Journal of Mathematics and Physics, vol. 17, no. 1-4, pp. 123– 199, 1938. [Online]. Available: http://dx.doi.org/10.1002/sapm1938171123
[4] A. J. Chorin, “Numerical study of slightly viscous flow,” Journal of Fluid Mechanics, vol. 57, no. 4, pp. 785–796, 1973.
[5] P. S. Bernard, “A Deterministic Vortex Sheet Method for Boundary Layer Flow,” Journal of Computational Physics, vol. 117, no. 1, pp. 132–145, 1995. [Online]. Available: http://www.sciencedirect.com/science/article/pii/ S0021999185710510
[6] V. Girault, “Theory of a finite difference method on irregular networks,” SIAM Journal on Numerical Analysis, vol. 11, no. 2, pp. 260–282, 1974. [Online]. Available: https://doi.org/10.1137/0711026
[7] V. Pavlin and N. Perrone, “Finite difference energy techniques for arbitrary meshes applied to linear plate problems,” International Journal for Numerical Methods in Engineering, vol. 14, no. 5, pp. 647–664, 1979. [Online]. Available: http://dx.doi.org/10.1002/nme.1620140503
[8] D. Vesey, C. Snell and P. Mullord, “The application of a general ffdm to some boundary value problems,” Composite Structures, no. 13, pp. 547–552, 1981.
[9] T.LiszkaandJ.Orkisz,Finite difference method at arbitrary irregular meshes in non-linear problems of applied mechanics. Structuralmechanicsinreactor technology, 1977, vol. 10, no. 12.
[10] J. Krok and J. Orkisz, A Unified Approach to the FE and Generalized Variational FD Methods in Nonlinear Mechanics, Concepts and Numerical Approach. Berlin, Heidelberg: Springer Berlin Heidelberg, 1990, pp. 353–362. [Online]. Available: https://doi.org/10.1007/978-3-642-49373-7_33
[11] L. B. Lucy, “A numerical approach to the testing of the fission hypothesis,” Astronomical Journal, vol. 82, pp. 1013–1024, Dec. 1977.
[12] J. Monaghan and J. Lattanzio, “A refined particle method for astrophysical problems,” Astronomy and Astrophysics, vol. 149, no. 1, pp. 135–143, 1985.
[13] R. A. Gingold and J. J. Monaghan, “Smoothed particle hydrodynamics: theory and application to non-spherical stars,” Monthly Notices of the Royal Astronomical Society, vol. 181, no. 3, pp. 375–389, 1977. [Online]. Available: http://dx.doi.org/10.1093/mnras/181.3.375
[14] G. Liu, Mesh Free Methods: Moving Beyond the Finite Element Method. CRC Press, 2002. [Online]. Available: https://books.google.com.co/books? id=61rMBQAAQBAJ
[15] B. Nayroles, G. Touzot, and P. Villon, “Generalizing the finite element method: Diffuse approximation and diffuse elements,” Computational Mechanics, vol. 10, no. 5, pp. 307–318, sep 1992. [Online]. Available: https://doi.org/10.1007/BF00364252
[16] T. Belytschko, Y. Y. Lu, and L. Gu, “Element-free Galerkin methods,” International Journal for Numerical Methods in Engineering, vol. 37, no. 2, pp. 229–256, 1994. [Online]. Available: http://dx.doi.org/10.1002/ nme.1620370205
[17] W. K. Liu, S. Jun, and Y. F. Zhang, “Reproducing kernel particle methods,” International Journal for Numerical Methods in Fluids, vol. 20, no. 8-9, pp. 1081–1106, 1995. [Online]. Available: http: //dx.doi.org/10.1002/fld.1650200824
[18] G. R. Liu and Y. T. Gu, “A local radial point interpolation method (lrpim) for free vibration analyses of 2-d solids,” Journal of Sound and Vibration, vol. 246, no. 1, pp. 29–46, 2001. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0022460X00936265
[19] S. N. Atluri and T. Zhu, “A new Meshless Local Petrov-Galerkin (MLPG) approach in computational mechanics,” Computational Mechanics, vol. 22, no. 2, pp. 117–127, 1998. [Online]. Available: https://doi.org/10.1007/ s004660050346
[20] Y. U. Xie Mukherjee and S. Mukherjee, “Boundary node method for potential problems,” International Journal for Numerical Methods in Engineering, vol. 40, pp. 797–815, 1997.
[21] G. R. Liu and Y. T. Gu, “Comparisons of two meshfree local point interpolation methods for structural analyses,” Computational Mechanics, vol. 29, no. 2, pp. 107–121, 2002. [Online]. Available: https://doi.org/10.1007/s00466-002-0320-4
[22] G. R. Liu and Y. T. Gu, “A meshfree method: meshfree weak–strong (MWS) form method, for 2-D solids,” Computational Mechanics, vol. 33, no. 1, pp. 2–14, 2003. [Online]. Available: https://doi.org/10.1007/s00466-003-0477-5
[23] G. R. Liu and Y. T. Gu, “A truly meshless method based on the strongweak form. advances in meshfree and x-fem methods,” in In Proceeding of the 1st Asian Workshop in Meshfree Methods, 2002.
[24] S. P. Timoshenko and J. N. Goodier, Theory of Elasticity, 3rd ed. New York, McGraw-Hill, 1970.
[25] R. David, “Introduction to elasticity,” Digital Module, january 2000. [Online]. Available: https://engkarrar.files.wordpress.com/2013/01/ david-roylance-mechanics-of-materials.pdf
[26] G. R. Liu and Y. T. Gu, An Introduction to Meshfree Methods and Their Programming. Springer Netherlands, 2005. [Online]. Available: https://books.google.com.co/books?id=0xS_2XlQ_Q0C
[27] P. Laurent, L. Mehaute, L. Schumaker, and W. Mass, “Approximation of polynomials by radial basis functions,” in In An international conference on curves and surfaces on Wavelets, images, and surface fitting, R. Schaback, Ed., 1994, pp. 459–466.
Article Sidebar
Article Details
Fabio H Realpe, Universidad del Cauca
Departamento de Electrónica, Instrumentación y Control, Universidad del Cauca.
Yasser H Ochoa, Universidad del Valle
Escuela de Ingeniería de Materiales, Universidad del Valle
Francisco Franco, Universidad del Cauca
Departamento de Electrónica, Instrumentación y Control, Universidad del Cauca
Pedro J Díaz, Universidad Industrial de Santander
Escuela de Ingeniería Mecánica, Universidad Industrial de Santander
Los autores que publican en esta revista están de acuerdo con los siguientes términos:
- Los autores conservan los derechos de autor y garantizan a la revista el derecho de ser la primera publicación del trabajo al igual que licenciado bajo una Creative Commons Attribution License que permite a otros compartir el trabajo con un reconocimiento de la autoría del trabajo y la publicación inicial en esta revista.
- Los autores pueden establecer por separado acuerdos adicionales para la distribución no exclusiva de la versión de la obra publicada en la revista (por ejemplo, situarlo en un repositorio institucional o publicarlo en un libro), con un reconocimiento de su publicación inicial en esta revista.
- Se permite y se anima a los autores a difundir sus trabajos electrónicamente (por ejemplo, en repositorios institucionales o en su propio sitio web) antes y durante el proceso de envío, ya que puede dar lugar a intercambios productivos, así como a una citación más temprana y mayor de los trabajos publicados (Véase The Effect of Open Access) (en inglés).