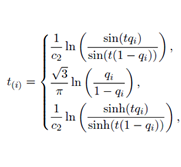Generalized Secant Hyperbolic and a Method of Estimate of its Parameters: Maximum Likelihood Modified
Main Article Content
Keywords
Generalized secant hyperbolic distribution, modified maximum likelihood, estimation of parameters.
Abstract
Different generalized distributions are developed in the statistical literature, among them it is the generalized secant hyperbolic distribution (SHG). This paper presents an alternative method for estimation the population parameters of the SHG, called Modified Maximum Likelihood (MVM). Assuming some alternate expressions that are different from Vaughan´s work in 2002, and based on the same set of data from the original source. It is implemented, the transformed method MVM is implemented computationally, it allows us to observe good approximations of the exact values of the parameters of location and scale, presented by Vaughan in his article. The aim is that in the practice you can use a different methodology to estimate.
MSC: 60E05, 62E10
Downloads
References
[2] J. Talacko, “Perks’ Distributions and Their Role in the Theory of Wiener’s Stochastic Variables,” Trabajos de Estadística, vol. 7, pp. 159–174, 1956.
[3] C. N. Morris, “Natural exponential families with quadratic variance functions,” The Annals of Statistics, vol. 10, pp. 65–80, 1982.
[4] D. C. Vaughan, “The Generalized Secant Hyperbolic Distribution And Its Properties,” Communications in statistics, vol. 31, no. 2, pp. 219–238, 2002.
[5] M. L. Tiku, D. Aysen, and Akkaya, Robust Estimation and Hypothesis Testing, 2nd ed. New York: New Age, 2004.
[6] M. Fischer and D. Vaughan, “Classes of skewed generalized secant hyperbolic distributions,” Universität Erlangen-Nürnberg: Lehrstuhl für Statistik und Ökonometrie, Tech. Rep, no. 45, 2002.
[7] C. Fernandez, J. Osiewalski, and M. F. J. Steel, “Modelling and inference with -spherical distributions,” Journal of American Statistical Association, vol. 90, pp. 1331–1340, 1995.
[8] M. Burbano, Tesis de pregrado, Universidad Distrital Francisco Jose de Caldas, Facultad de Ciencias y Educación. Departamento de Matemáticas, Bogotá, Colombia, 2012.
[9] V. D. Barnett, “Evaluation of the maximum likelihood estimator when the likelihood equation has multiple roots,” Biometrika, vol. 53, pp. 151–165, 1996a.
[10] M. L. Tiku and R. P. Suresh, “A new method of estimation for location and scale parameters,” J. Stat. Plann, vol. 30, pp. 281–292, 1992.
[11] S. Puthenpura and N. K. Sinha, “Modified maximum likelihood method for the robust estimation of system parametrs from very noisy data,” Automatica, vol. 22, pp. 231–235, 1986.
[12] M. L. Tiku, “Estimating the mean and Standard Deviation from a censored Normal Sample,” Biometrika, vol. 54, no. 1, pp. 155–165, 1967a.
[13] M. Tiku, “A note on estimating the location and scale parameters of the exponential distribution from a censored sample,” Austral. J. Statist, vol. 9, no. 1, pp. 49–54, 1967b.
[14] M. L. Tiku, W. K. Wong, D. C. Vaughan, and G. Bian, “Time series models in non-normal situations: symmetric innovations,” J. Time Series Analysis, vol. 21, pp. 571–596, 2000.
[15] R. A. Fisher, The Design of Experimets, 9th ed. Hafner Publishing company, 1971.