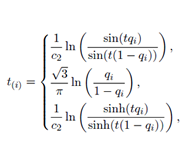Generalized Secant Hyperbolic and a Method of Estimate of its Parameters: Maximum Likelihood Modified
Main Article Content
Keywords
Generalized secant hyperbolic distribution, modified maximum likelihood, estimation of parameters.
Abstract
Different generalized distributions are developed in the statistical literature, among them it is the generalized secant hyperbolic distribution (SHG). This paper presents an alternative method for estimation the population parameters of the SHG, called Modified Maximum Likelihood (MVM). Assuming some alternate expressions that are different from Vaughan´s work in 2002, and based on the same set of data from the original source. It is implemented, the transformed method MVM is implemented computationally, it allows us to observe good approximations of the exact values of the parameters of location and scale, presented by Vaughan in his article. The aim is that in the practice you can use a different methodology to estimate.
MSC: 60E05, 62E10
Downloads
References
[2] J. Talacko, “Perks’ Distributions and Their Role in the Theory of Wiener’s Stochastic Variables,” Trabajos de Estadística, vol. 7, pp. 159–174, 1956.
[3] C. N. Morris, “Natural exponential families with quadratic variance functions,” The Annals of Statistics, vol. 10, pp. 65–80, 1982.
[4] D. C. Vaughan, “The Generalized Secant Hyperbolic Distribution And Its Properties,” Communications in statistics, vol. 31, no. 2, pp. 219–238, 2002.
[5] M. L. Tiku, D. Aysen, and Akkaya, Robust Estimation and Hypothesis Testing, 2nd ed. New York: New Age, 2004.
[6] M. Fischer and D. Vaughan, “Classes of skewed generalized secant hyperbolic distributions,” Universität Erlangen-Nürnberg: Lehrstuhl für Statistik und Ökonometrie, Tech. Rep, no. 45, 2002.
[7] C. Fernandez, J. Osiewalski, and M. F. J. Steel, “Modelling and inference with -spherical distributions,” Journal of American Statistical Association, vol. 90, pp. 1331–1340, 1995.
[8] M. Burbano, Tesis de pregrado, Universidad Distrital Francisco Jose de Caldas, Facultad de Ciencias y Educación. Departamento de Matemáticas, Bogotá, Colombia, 2012.
[9] V. D. Barnett, “Evaluation of the maximum likelihood estimator when the likelihood equation has multiple roots,” Biometrika, vol. 53, pp. 151–165, 1996a.
[10] M. L. Tiku and R. P. Suresh, “A new method of estimation for location and scale parameters,” J. Stat. Plann, vol. 30, pp. 281–292, 1992.
[11] S. Puthenpura and N. K. Sinha, “Modified maximum likelihood method for the robust estimation of system parametrs from very noisy data,” Automatica, vol. 22, pp. 231–235, 1986.
[12] M. L. Tiku, “Estimating the mean and Standard Deviation from a censored Normal Sample,” Biometrika, vol. 54, no. 1, pp. 155–165, 1967a.
[13] M. Tiku, “A note on estimating the location and scale parameters of the exponential distribution from a censored sample,” Austral. J. Statist, vol. 9, no. 1, pp. 49–54, 1967b.
[14] M. L. Tiku, W. K. Wong, D. C. Vaughan, and G. Bian, “Time series models in non-normal situations: symmetric innovations,” J. Time Series Analysis, vol. 21, pp. 571–596, 2000.
[15] R. A. Fisher, The Design of Experimets, 9th ed. Hafner Publishing company, 1971.
Article Sidebar
Article Details
Luis Alejandro Másmela Caita, Universidad Distrital Francisco José de Caldas
Magíster en estadísticaÁlvaro Alexander Burbano Moreno, Universidad Distrital Francisco Jose de Caldas.
Estudiante de maestría en estadística, Universidad Nacional de Colombia
Authors who publish with this journal agree to the following terms:
- Authors retain copyright and grant the journal right of first publication with the work simultaneously licensed under a Creative Commons Attribution License that allows others to share the work with an acknowledgement of the work's authorship and initial publication in this journal.
- Authors are able to enter into separate, additional contractual arrangements for the non-exclusive distribution of the journal's published version of the work (e.g., post it to an institutional repository or publish it in a book), with an acknowledgement of its initial publication in this journal.
- Authors are permitted and encouraged to post their work online (e.g., in institutional repositories or on their website) prior to and during the submission process, as it can lead to productive exchanges, as well as earlier and greater citation of published work (See The Effect of Open Access).