K-deformed conic sections
Main Article Content
Keywords
K-deformed sum and difference, K-deformed ellipse, K-deformed circle, K-deformed parabola, K-deformed hyperbola
Abstract
In this paper we study the effects of the K-deformed sum, defined as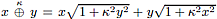 
on the Euclidean distance function d(P, F1) + d(P, F2) = 2a, where P is an arbitrary point in R2 ; F1 and F2 are the focus of the curve named Ellipse. The points satisfying the resulting equality d(P, F1) 
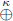d(P, F2) = 2a, describe a curve named K-deformed ellipse for which the resulting analityc expression is analogue to the standard one. We make a deep study of the vertex, local extrema, asymptotes, the latus rectum and the graph of the resulting K-deformed conic ections: Ellipse, hyperbola, circumference and parábola in the K-deformed setting. We also make a study of the area of the regions limited by the -deformed ellipse and hyperbola for an arbitrary value of K.
Downloads
References
[2] P. Costa Buján, “Superficies cónicas: Aplicación a la arquitectura y el diseño[vídeo],” 2014. [Online]. Available: http://hdl.handle.net/2183/12666 10
[3] P. Ramírez Granados, “Elementos de cartografía matemática y su aplicaciónen la elaboración de las cartas geográficas,” Revista Geográfica deAmérica Central, vol. 46, no. 1, pp. 15–36, 2011. [Online]. Available: http://www.revistas.una.ac.cr/index.php/geografica/article/view/3290 10
[4] M. González and G. Patiño, “Método para obtener los elementosde las secciones cónicas por medio de la derivación implícita,”TecnoLógicas, no. 19, pp. 87–118, 2007. [Online]. Available: http://itmojs.itm.edu.co/index.php/tecnologicas/article/view/305 10
[5] C. Lehmann, “Geometría Analítica,” Noriega Editores, 1995. 11
[6] M. Karatas, “A multi foci closed curve: Cassini oval, its properties and applications,” Doğuş University Dergisi, vol. 2, no. 14, pp. 231–248, 2013. [Online]. Available: http://journal.dogus.edu.tr/index.php/duj/article/view/661 11
[7] G. Kaniadakis, “Statistical mechanics in the context of special relativity,”The American Physical Society, hysical Review E, no. 66, pp. 1–17, 2002.[Online]. Available: https://dx.doi.org/10.1103/PhysRevE.66.056125 11
[8] ——, “Statistical mechanics in the context of special relativity II,” TheAmerican Physical Society, Physical Review E, no. 72, pp. 1–14, 2005.[Online]. Available: https://dx.doi.org/10.1103/PhysRevE.72.036108 11
[9] D. Deossa, “Sobre funciones exponenciales y logarítmicas deformadassegún Kaniadakis,” p. 96, 2011. [Online]. Available:http://hdl.handle.net/10784/156 11
[10] J. C. Arango Parra, “Una variedad de información estadística -deformada,” p. 121, 2012. [Online]. Available: http://hdl.handle.net/10784/1307 11
[11] H. Quiceno and J. C. Arango, “K-exponential Statistical Manifold Modeled on Orlicz Spaces,” Journal of Mathematical Analysis and Applications, vol. 2, no. 431, pp. 1080–1098, 2015. [Online]. Available: http://dx.doi.org/10.1016/j.jmaa.2015.05.065 11
[12] J. Ramírez and Y. Hernández, “La matriz -exponencial y soluciones de algunos sistemas de ecuaciones diferenciales,” Tesis de Maestría, Universidad Eafit, p. 82, 2014. [Online]. Available: http://hdl.handle.net/10784/8108 11
[13] C. Tsallis, “Possible generalization of Boltzmann-Gibbs statistics,” Journal of Statistical Physics, vol. 52, no. 1, pp. 479–487, 1988. [Online]. Available: http://dx.doi.org/10.1007/BF01016429 27
[14] G. Loaiza and H. Quiceno, “A q-exponential statistical Banach Manifold,” Journal of Mathematical Analysis and Applica-
tions, vol. 2, no. 398, pp. 466–476, 2013. [Online]. Available: http://dx.doi.org/10.1016/S0378-4371(02)01018-X 27
[15] J. Naudts, “Deformed exponentials and logarithms in generalized thermostatics,” Physica A. Statistical Mechanics and its Applications, vol. 1-4, no. 316, pp. 323–334, 2002. [Online]. Available: http://dx.doi.org/10.1016/S0378-4371(02)01018-X 27
[16] H. Quiceno Echavarría, “Variedad de información estadística q-exponencial,” p. 73, 2010. [Online]. Available: http://hdl.handle.net/10784/153 27