Secciones cónicas k-deformadas
Main Article Content
Keywords
Suma y diferencia k-deformada, elipse k-deformada, circunferencia k-deformada, parábola k-deformada, hipérbola k-deformada
Resumen
En el presente artículo se analiza el efecto que tiene sobre la igualdad d(P, F1) + d(P, F2)=2a siendo P un punto del plano, F1 y F2 los focos de esta figura plana llamada elipse y a una constante positiva, el uso de la suma k-deformada en el sentido de Kaniadakis, la cual se define como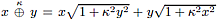 
para 0 < k < 1. La igualdad resultante d(P, F1) 
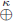d(P, F2) = 2a recibe el nombre de elipse K-deformada y tiene ecuaciones análogas a las de la elipse definida en el sentido usual. En el artículo se hace el estudio sobre los vértices, los extremos relativos, las asíntotas, el lado recto, la representación gráfica para las cuatro secciones cónicas: elipse, hipérbola, circunferencia y parábola en el sentido K-deformado. Se estudia también el área que encierran la elipse y la hipérbola para cualquier valor de K.
Descargas
Referencias
[2] P. Costa Buján, “Superficies cónicas: Aplicación a la arquitectura y el diseño[vídeo],” 2014. [Online]. Available: http://hdl.handle.net/2183/12666 10
[3] P. Ramírez Granados, “Elementos de cartografía matemática y su aplicaciónen la elaboración de las cartas geográficas,” Revista Geográfica deAmérica Central, vol. 46, no. 1, pp. 15–36, 2011. [Online]. Available: http://www.revistas.una.ac.cr/index.php/geografica/article/view/3290 10
[4] M. González and G. Patiño, “Método para obtener los elementosde las secciones cónicas por medio de la derivación implícita,”TecnoLógicas, no. 19, pp. 87–118, 2007. [Online]. Available: http://itmojs.itm.edu.co/index.php/tecnologicas/article/view/305 10
[5] C. Lehmann, “Geometría Analítica,” Noriega Editores, 1995. 11
[6] M. Karatas, “A multi foci closed curve: Cassini oval, its properties and applications,” Doğuş University Dergisi, vol. 2, no. 14, pp. 231–248, 2013. [Online]. Available: http://journal.dogus.edu.tr/index.php/duj/article/view/661 11
[7] G. Kaniadakis, “Statistical mechanics in the context of special relativity,”The American Physical Society, hysical Review E, no. 66, pp. 1–17, 2002.[Online]. Available: https://dx.doi.org/10.1103/PhysRevE.66.056125 11
[8] ——, “Statistical mechanics in the context of special relativity II,” TheAmerican Physical Society, Physical Review E, no. 72, pp. 1–14, 2005.[Online]. Available: https://dx.doi.org/10.1103/PhysRevE.72.036108 11
[9] D. Deossa, “Sobre funciones exponenciales y logarítmicas deformadassegún Kaniadakis,” p. 96, 2011. [Online]. Available:http://hdl.handle.net/10784/156 11
[10] J. C. Arango Parra, “Una variedad de información estadística -deformada,” p. 121, 2012. [Online]. Available: http://hdl.handle.net/10784/1307 11
[11] H. Quiceno and J. C. Arango, “K-exponential Statistical Manifold Modeled on Orlicz Spaces,” Journal of Mathematical Analysis and Applications, vol. 2, no. 431, pp. 1080–1098, 2015. [Online]. Available: http://dx.doi.org/10.1016/j.jmaa.2015.05.065 11
[12] J. Ramírez and Y. Hernández, “La matriz -exponencial y soluciones de algunos sistemas de ecuaciones diferenciales,” Tesis de Maestría, Universidad Eafit, p. 82, 2014. [Online]. Available: http://hdl.handle.net/10784/8108 11
[13] C. Tsallis, “Possible generalization of Boltzmann-Gibbs statistics,” Journal of Statistical Physics, vol. 52, no. 1, pp. 479–487, 1988. [Online]. Available: http://dx.doi.org/10.1007/BF01016429 27
[14] G. Loaiza and H. Quiceno, “A q-exponential statistical Banach Manifold,” Journal of Mathematical Analysis and Applica-
tions, vol. 2, no. 398, pp. 466–476, 2013. [Online]. Available: http://dx.doi.org/10.1016/S0378-4371(02)01018-X 27
[15] J. Naudts, “Deformed exponentials and logarithms in generalized thermostatics,” Physica A. Statistical Mechanics and its Applications, vol. 1-4, no. 316, pp. 323–334, 2002. [Online]. Available: http://dx.doi.org/10.1016/S0378-4371(02)01018-X 27
[16] H. Quiceno Echavarría, “Variedad de información estadística q-exponencial,” p. 73, 2010. [Online]. Available: http://hdl.handle.net/10784/153 27