Evaluación leave-one-out de los clasificadores de la línea de características más cercana y del segmento de línea rectificado más cercano usando arquitecturas multi-núcleo
Main Article Content
Keywords
Computación con múltiples núcleos, algoritmos de clasificación, prueba leave-one-out
Resumen
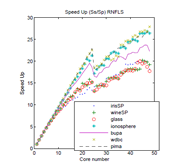
Presentamos en este artículo la paralelización de la prueba leave-one-out, la cual es una prueba repetible pero que, en general, resulta costosa computacionalmente. La paralelización se implementó sobre arquitecturas multinúcleo con múltiples hilos, usando la taxonomía Flynn Single Instruction Multiple Data. Esta técnica se empleó para las etapas de preproceso y proceso de dos algoritmos de clasificación que están orientados a enriquecer la representación en casos de muestra pequeña: el algoritmo de la línea de características más cercana (NFL) y el algoritmo del segmento de línea rectificado más cercano (RNFLS). Los resultados obtenidos muestran una aceleración de hasta 18.17 veces con el conjunto de datos mas pequeño y de 29.91 veces con el conjunto de datos más grande, empleando el algoritmo más costoso —RNFLS— cuya complejidad es O(n4). El artículo muestra también los pseudocódigos de los algoritmos seriales y paralelos empleando, en este último caso, una notación que describe la manera como se realizó la paralelización en función de los hilos.
Descargas
Referencias
[2] R. P. W. Duin, M. Bicego, M. Orozco-Alzate, S.-W. Kim, andM. Loog, “Metric Learning in Dissimilarity Space for Improved NearestNeighbor Performance,” inStructural, Syntactic and Statistical PatternRecognition: Proceedings of the Joint IAPR International Workshop,S+SSPR 2014, ser. Lecture Notes in Computer Science, P. Fränti,G. Brown, M. Loog, F. Escolano, and M. Pelillo, Eds., vol. 8621,IAPR. Berlin Heidelberg: Springer, 2014, pp. 183–192. [Online]. Available:https://doi.org/10.1007/978-3-662-44415-3{_}19 77
[3] S. Z. Li and J. Lu, “Face Recognition Using the Nearest Feature LineMethod,”IEEE Transactions on Neural Networks, vol. 10, no. 2, pp. 439–443,1999. 77, 79
[4] H. Du and Y. Q. Chen, “Rectified nearest feature line segment for patternclassification,”Pattern Recognition, vol. 40, no. 5, pp. 1486–1497, 2007.[Online]. Available: https://doi.org/10.1016/j.patcog.2006.10.021 77, 82
[5] J. Gama, I. Žliobait ̇e, A. Bifet, M. Pechenizkiy, and A. Bouchachia, “A Sur-vey on Concept Drift Adaptation,”ACM Computing Surveys, vol. 46, no. 4,pp. 44:1—-44:37, mar 2014. 77
[6] M. Bramer,Principles of Data Mining, 2nd ed., ser. Undergraduate Topicsin Computer Science. London, UK: Springer, 2013. 77
[7] B. Clarke, E. Fokoué, and H. H. Zhang,Principles and Theory for DataMining and Machine Learning, ser. Springer Series in Statistics. New York,NY: Springer New York, 2009. 78
[8] N. Lopes and B. Ribeiro,Machine Learning for Adaptive Many-Core Ma-chines - A Practical Approach, ser. Studies in Big Data. Cham, Switzerland:Springer International Publishing, 2015, vol. 7. 78
[9] A. Ahmadzadeh, R. Mirzaei, H. Madani, M. Shobeiri, M. Sadeghi, M. Gavahi,K. Jafari, M. M. Aznaveh, and S. Gorgin, “Cost-efficient implementationof k-NN algorithm on multi-core processors,” inTwelfth ACM/IEEE Inter-national Conference on Formal Methods and Models for Codesign, MEM-OCODE 2014, oct 2014, pp. 205–208. 78
[10] V. D. Katkar and S. V. Kulkarni, “A novel parallel implementationof Naive Bayesian classifier for Big Data,” inInternational Conferenceon Green Computing, Communication and Conservation of Energy, ICGCE 2013. IEEE, 2013, pp. 847–852. [Online]. Available: https://doi.org/10.1109/ICGCE.2013.6823552 78
[11] Y. You, H. Fu, S. L. Song, A. Randles, D. Kerbyson, A. Marquez,G. Yang, and A. Hoisie, “Scaling Support Vector Machines on modern HPCplatforms,”Journal of Parallel and Distributed Computing, vol. 76, pp.16–31, 2015. [Online]. Available: https://doi.org/10.1016/j.jpdc.2014.09.00578
[12] A.-L. Uribe-Hurtado and M. Orozco-Alzate, “Acceleration of Dissimilarity-Based Classification Algorithms Using Multi-core Computation,” inTrendsin Cyber-Physical Multi-Agent Systems. The PAAMS Collection - 15th In-ternational Conference, PAAMS 2017, ser. Advances in Intelligent Systemsand Computing, A. T. Campbell, F. de la Prieta, Z. Vale, L. Antunes, M. N Moreno, V. Julian, T. Pinto, and A. J. R. Neves, Eds., vol. 619, IEEE SystemsMan and Cybernetics Society Spain Section Chapter. Cham, Switzerland:Springer, jun 2017, pp. 231–233. 78
[13] E. Pekalska and R. P. W. Duin, “Dissimilarity representations allow forbuilding good classifiers,”Pattern Recognition Letters, vol. 23, no. 8, pp.943–956, 2002. [Online]. Available: https://doi.org/10.1016/S0167-8655(02)00024-7 79
[14] H. Che and M. Nguyen, “Amdahl’s law for multithreaded multicoreprocessors,”Journal of Parallel and Distributed Computing, vol. 74, no. 10,pp. 3056–3069, 2014. [Online]. Available: https://doi.org/10.1016/j.jpdc.2014.06.012 94
[15] J. Nutaro and B. Zeigler, “How to apply Amdahl’s law to multithreadedmulticore processors,”Journal of Parallel and Distributed Computing, vol.107, no. Supplement C, pp. 1–2, 2017. 94
Article Sidebar
Article Details
Los autores que publican en esta revista están de acuerdo con los siguientes términos:
- Los autores conservan los derechos de autor y garantizan a la revista el derecho de ser la primera publicación del trabajo al igual que licenciado bajo una Creative Commons Attribution License que permite a otros compartir el trabajo con un reconocimiento de la autoría del trabajo y la publicación inicial en esta revista.
- Los autores pueden establecer por separado acuerdos adicionales para la distribución no exclusiva de la versión de la obra publicada en la revista (por ejemplo, situarlo en un repositorio institucional o publicarlo en un libro), con un reconocimiento de su publicación inicial en esta revista.
- Se permite y se anima a los autores a difundir sus trabajos electrónicamente (por ejemplo, en repositorios institucionales o en su propio sitio web) antes y durante el proceso de envío, ya que puede dar lugar a intercambios productivos, así como a una citación más temprana y mayor de los trabajos publicados (Véase The Effect of Open Access) (en inglés).